Load packages + data
# load packages
devtools::install_github("MomX/Momocs")
## Skipping install of 'Momocs' from a github remote, the SHA1 (e7ba9b88) has not changed since last install.
## Use `force = TRUE` to force installation
library(here)
library(Momocs)
# read images
jpg.list <- list.files(here("img.perdiz"), full.names = TRUE)
# read attribute data
att.data <- read.csv("perdiz.csv", header = TRUE, as.is = TRUE)
# attribute to factor
att.data$region <- as.factor(att.data$region)
att.data$temp.reg <- as.factor(att.data$temp.reg)
knitr::kable((att.data[, 1:5]), "pipe", caption = "Qualitative data for Perdiz arrow point sample.")
(#tab:load.packages)Qualitative data for Perdiz arrow point sample.
| 489 |
41cp20 |
LC |
north |
LCN |
| 490 |
41cp20 |
LC |
north |
LCN |
| 553 |
41cp12 |
LC |
north |
LCN |
| 554 |
41cp12 |
LC |
north |
LCN |
| 555 |
41cp12 |
LC |
north |
LCN |
| 556 |
41cp12 |
LC |
north |
LCN |
| 558 |
41cp12 |
LC |
north |
LCN |
| 559 |
41cp12 |
LC |
north |
LCN |
| 562 |
41cp12 |
LC |
north |
LCN |
| 565 |
41cp12 |
LC |
north |
LCN |
| 591 |
41cp12 |
LC |
north |
LCN |
| 598 |
41cp5 |
LC |
north |
LCN |
| 645 |
41cp5 |
LC |
north |
LCN |
| 646 |
41cp5 |
LC |
north |
LCN |
| 647 |
41cp5 |
LC |
north |
LCN |
| 648 |
41cp5 |
LC |
north |
LCN |
| 649 |
41cp5 |
LC |
north |
LCN |
| 650 |
41cp5 |
LC |
north |
LCN |
| 651 |
41cp5 |
LC |
north |
LCN |
| 652 |
41cp5 |
LC |
north |
LCN |
| 653 |
41cp5 |
LC |
north |
LCN |
| 654 |
41cp5 |
LC |
north |
LCN |
| 655 |
41cp5 |
LC |
north |
LCN |
| 656 |
41cp5 |
LC |
north |
LCN |
| 657 |
41cp5 |
LC |
north |
LCN |
| 658 |
41cp5 |
LC |
north |
LCN |
| 659 |
41cp5 |
LC |
north |
LCN |
| 660 |
41cp5 |
LC |
north |
LCN |
| 661 |
41cp5 |
LC |
north |
LCN |
| 665 |
41cp12 |
LC |
north |
LCN |
| 677 |
41cp20 |
LC |
north |
LCN |
| 678 |
41cp20 |
LC |
north |
LCN |
| an51-fig26a |
41an51 |
MC |
south |
MCS |
| an51-fig26c |
41an51 |
MC |
south |
MCS |
| an115-fig7 |
41an115 |
MC |
south |
MCS |
| cp220-fig11-12a |
41cp220 |
LC |
north |
LCN |
| cp495-fig16h |
41cp495 |
LC |
north |
LCN |
| cp495-fig16i |
41cp495 |
LC |
north |
LCN |
| hc2-fig30a |
hcreek2 |
MC |
south |
MCS |
| hc2-fig30b |
hcreek2 |
MC |
south |
MCS |
| hc2-fig30c |
hcreek2 |
MC |
south |
MCS |
| hc2-fig30d |
hcreek2 |
MC |
south |
MCS |
| hc2-fig30f |
hcreek2 |
MC |
south |
MCS |
| hc2-fig30h |
hcreek2 |
MC |
south |
MCS |
| hc2-fig30i |
hcreek2 |
MC |
south |
MCS |
| hc2-fig30l |
hcreek2 |
MC |
south |
MCS |
| hc2-fig30m |
hcreek2 |
MC |
south |
MCS |
| hc2-fig30n |
hcreek2 |
MC |
south |
MCS |
| hs15-fig7.1r |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.1t |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.1u |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.1v |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.1w |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.1x |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.2b |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.2c |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.2d |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.2e |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.2f |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.2g |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.2m |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.2o |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.2q |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.2r |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3a |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3aa |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3b |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3bb |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3cc |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3d |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3e |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3f |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3g |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3h |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3i |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3j |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3k |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3l |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3m |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3n |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3o |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3p |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3q |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3r |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3s |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3t |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3u |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3w |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3x |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3y |
41hs15 |
LC |
north |
LCN |
| hs15-fig7.3z |
41hs15 |
LC |
north |
LCN |
| hs235-fig17 |
41hs235 |
LC |
north |
LCN |
| hs269-fig12j |
41hs269 |
MC |
north |
MCN |
| na206-fig12a |
41na206 |
HC |
south |
HCS |
| na206-fig12b |
41na206 |
HC |
south |
HCS |
| na206-fig12d |
41na206 |
HC |
south |
HCS |
| na206-fig12f |
41na206 |
HC |
south |
HCS |
| na206-fig12g |
41na206 |
HC |
south |
HCS |
| na49-1 |
41na49 |
MC |
south |
MCS |
| na49-10 |
41na49 |
MC |
south |
MCS |
| na49-11 |
41na49 |
MC |
south |
MCS |
| na49-12 |
41na49 |
MC |
south |
MCS |
| na49-13 |
41na49 |
MC |
south |
MCS |
| na49-137 |
41na49 |
MC |
south |
MCS |
| na49-14 |
41na49 |
MC |
south |
MCS |
| na49-149 |
41na49 |
MC |
south |
MCS |
| na49-176 |
41na49 |
MC |
south |
MCS |
| na49-187 |
41na49 |
MC |
south |
MCS |
| na49-195 |
41na49 |
MC |
south |
MCS |
| na49-2 |
41na49 |
MC |
south |
MCS |
| na49-271 |
41na49 |
MC |
south |
MCS |
| na49-3 |
41na49 |
MC |
south |
MCS |
| na49-33 |
41na49 |
MC |
south |
MCS |
| na49-4 |
41na49 |
MC |
south |
MCS |
| na49-5 |
41na49 |
MC |
south |
MCS |
| na49-587 |
41na49 |
MC |
south |
MCS |
| na49-616 |
41na49 |
MC |
south |
MCS |
| na49-7 |
41na49 |
MC |
south |
MCS |
| na49-734 |
41na49 |
MC |
south |
MCS |
| na49-8 |
41na49 |
MC |
south |
MCS |
| na49-9 |
41na49 |
MC |
south |
MCS |
| sa135-fig15b |
41sa135 |
MC |
south |
MCS |
| sa135-fig15c |
41sa135 |
MC |
south |
MCS |
| sa135-fig15g |
41sa135 |
MC |
south |
MCS |
| sm193-fig1e |
41sm193 |
MC |
north |
MCN |
| sm193-fig2a |
41sm193 |
MC |
north |
MCN |
| sm193-fig2b |
41sm193 |
MC |
north |
MCN |
| sm193-fig2e |
41sm193 |
MC |
north |
MCN |
| sm193-fig2f |
41sm193 |
MC |
north |
MCN |
| sm193-fig2g |
41sm193 |
MC |
north |
MCN |
| sm195-fig8 |
41sm195 |
MC |
north |
MCN |
| sm442-fig19c |
41sm442 |
MC |
north |
MCN |
| sm55-fig23 |
41sm55 |
MC |
north |
MCN |
| sy280-1 |
41sy280 |
LC |
south |
LCS |
| sy280-2 |
41sy280 |
LC |
south |
LCS |
| sy280-3 |
41sy280 |
LC |
south |
LCS |
| sy43-1 |
41sy43 |
LC |
south |
LCS |
| sy43-2 |
41sy43 |
LC |
south |
LCS |
| sy43-3 |
41sy43 |
LC |
south |
LCS |
| sy43-4 |
41sy43 |
LC |
south |
LCS |
| sy43-5 |
41sy43 |
LC |
south |
LCS |
| sy43-6 |
41sy43 |
LC |
south |
LCS |
Generate outlines
# generate outlines
outlines <- jpg.list %>%
import_jpg()
## Extracting 142.jpg outlines...
## [ 1 / 142 ] 489.jpg
## [ 2 / 142 ] 490.jpg
## [ 3 / 142 ] 553.jpg
## [ 4 / 142 ] 554.jpg
## [ 5 / 142 ] 555.jpg
## [ 6 / 142 ] 556.jpg
## [ 7 / 142 ] 558.jpg
## [ 8 / 142 ] 559.jpg
## [ 9 / 142 ] 562.jpg
## [ 10 / 142 ] 565.jpg
## [ 11 / 142 ] 591.jpg
## [ 12 / 142 ] 598.jpg
## [ 13 / 142 ] 645.jpg
## [ 14 / 142 ] 646.jpg
## [ 15 / 142 ] 647.jpg
## [ 16 / 142 ] 648.jpg
## [ 17 / 142 ] 649.jpg
## [ 18 / 142 ] 650.jpg
## [ 19 / 142 ] 651.jpg
## [ 20 / 142 ] 652.jpg
## [ 21 / 142 ] 653.jpg
## [ 22 / 142 ] 654.jpg
## [ 23 / 142 ] 655.jpg
## [ 24 / 142 ] 656.jpg
## [ 25 / 142 ] 657.jpg
## [ 26 / 142 ] 658.jpg
## [ 27 / 142 ] 659.jpg
## [ 28 / 142 ] 660.jpg
## [ 29 / 142 ] 661.jpg
## [ 30 / 142 ] 665.jpg
## [ 31 / 142 ] 677.jpg
## [ 32 / 142 ] 678.jpg
## [ 33 / 142 ] an115-fig7.jpg
## [ 34 / 142 ] an51-fig26a.jpg
## [ 35 / 142 ] an51-fig26c.jpg
## [ 36 / 142 ] cp220-fig11-12a.jpg
## [ 37 / 142 ] cp495-fig16h.jpg
## [ 38 / 142 ] cp495-fig16i.jpg
## [ 39 / 142 ] hc2-fig30a.jpg
## [ 40 / 142 ] hc2-fig30b.jpg
## [ 41 / 142 ] hc2-fig30c.jpg
## [ 42 / 142 ] hc2-fig30d.jpg
## [ 43 / 142 ] hc2-fig30f.jpg
## [ 44 / 142 ] hc2-fig30h.jpg
## [ 45 / 142 ] hc2-fig30i.jpg
## [ 46 / 142 ] hc2-fig30l.jpg
## [ 47 / 142 ] hc2-fig30m.jpg
## [ 48 / 142 ] hc2-fig30n.jpg
## [ 49 / 142 ] hs15-fig7.1r.jpg
## [ 50 / 142 ] hs15-fig7.1t.jpg
## [ 51 / 142 ] hs15-fig7.1u.jpg
## [ 52 / 142 ] hs15-fig7.1v.jpg
## [ 53 / 142 ] hs15-fig7.1w.jpg
## [ 54 / 142 ] hs15-fig7.1x.jpg
## [ 55 / 142 ] hs15-fig7.2b.jpg
## [ 56 / 142 ] hs15-fig7.2c.jpg
## [ 57 / 142 ] hs15-fig7.2d.jpg
## [ 58 / 142 ] hs15-fig7.2e.jpg
## [ 59 / 142 ] hs15-fig7.2f.jpg
## [ 60 / 142 ] hs15-fig7.2g.jpg
## [ 61 / 142 ] hs15-fig7.2m.jpg
## [ 62 / 142 ] hs15-fig7.2o.jpg
## [ 63 / 142 ] hs15-fig7.2q.jpg
## [ 64 / 142 ] hs15-fig7.2r.jpg
## [ 65 / 142 ] hs15-fig7.3a.jpg
## [ 66 / 142 ] hs15-fig7.3aa.jpg
## [ 67 / 142 ] hs15-fig7.3b.jpg
## [ 68 / 142 ] hs15-fig7.3bb.jpg
## [ 69 / 142 ] hs15-fig7.3cc.jpg
## [ 70 / 142 ] hs15-fig7.3d.jpg
## [ 71 / 142 ] hs15-fig7.3e.jpg
## [ 72 / 142 ] hs15-fig7.3f.jpg
## [ 73 / 142 ] hs15-fig7.3g.jpg
## [ 74 / 142 ] hs15-fig7.3h.jpg
## [ 75 / 142 ] hs15-fig7.3i.jpg
## [ 76 / 142 ] hs15-fig7.3j.jpg
## [ 77 / 142 ] hs15-fig7.3k.jpg
## [ 78 / 142 ] hs15-fig7.3l.jpg
## [ 79 / 142 ] hs15-fig7.3m.jpg
## [ 80 / 142 ] hs15-fig7.3n.jpg
## [ 81 / 142 ] hs15-fig7.3o.jpg
## [ 82 / 142 ] hs15-fig7.3p.jpg
## [ 83 / 142 ] hs15-fig7.3q.jpg
## [ 84 / 142 ] hs15-fig7.3r.jpg
## [ 85 / 142 ] hs15-fig7.3s.jpg
## [ 86 / 142 ] hs15-fig7.3t.jpg
## [ 87 / 142 ] hs15-fig7.3u.jpg
## [ 88 / 142 ] hs15-fig7.3w.jpg
## [ 89 / 142 ] hs15-fig7.3x.jpg
## [ 90 / 142 ] hs15-fig7.3y.jpg
## [ 91 / 142 ] hs15-fig7.3z.jpg
## [ 92 / 142 ] hs235-fig17.jpg
## [ 93 / 142 ] hs269-fig12j.jpg
## [ 94 / 142 ] na206-fig12a.jpg
## [ 95 / 142 ] na206-fig12b.jpg
## [ 96 / 142 ] na206-fig12d.jpg
## [ 97 / 142 ] na206-fig12f.jpg
## [ 98 / 142 ] na206-fig12g.jpg
## [ 99 / 142 ] na49-1.jpg
## [ 100 / 142 ] na49-10.jpg
## [ 101 / 142 ] na49-11.jpg
## [ 102 / 142 ] na49-12.jpg
## [ 103 / 142 ] na49-13.jpg
## [ 104 / 142 ] na49-137.jpg
## [ 105 / 142 ] na49-14.jpg
## [ 106 / 142 ] na49-149.jpg
## [ 107 / 142 ] na49-176.jpg
## [ 108 / 142 ] na49-187.jpg
## [ 109 / 142 ] na49-195.jpg
## [ 110 / 142 ] na49-2.jpg
## [ 111 / 142 ] na49-271.jpg
## [ 112 / 142 ] na49-3.jpg
## [ 113 / 142 ] na49-33.jpg
## [ 114 / 142 ] na49-4.jpg
## [ 115 / 142 ] na49-5.jpg
## [ 116 / 142 ] na49-587.jpg
## [ 117 / 142 ] na49-616.jpg
## [ 118 / 142 ] na49-7.jpg
## [ 119 / 142 ] na49-734.jpg
## [ 120 / 142 ] na49-8.jpg
## [ 121 / 142 ] na49-9.jpg
## [ 122 / 142 ] sa135-fig15b.jpg
## [ 123 / 142 ] sa135-fig15c.jpg
## [ 124 / 142 ] sa135-fig15g.jpg
## [ 125 / 142 ] sm193-fig1e.jpg
## [ 126 / 142 ] sm193-fig2a.jpg
## [ 127 / 142 ] sm193-fig2b.jpg
## [ 128 / 142 ] sm193-fig2e.jpg
## [ 129 / 142 ] sm193-fig2f.jpg
## [ 130 / 142 ] sm193-fig2g.jpg
## [ 131 / 142 ] sm195-fig8.jpg
## [ 132 / 142 ] sm442-fig19c.jpg
## [ 133 / 142 ] sm55-fig23.jpg
## [ 134 / 142 ] sy280-1.jpg
## [ 135 / 142 ] sy280-2.jpg
## [ 136 / 142 ] sy280-3.jpg
## [ 137 / 142 ] sy43-1.jpg
## [ 138 / 142 ] sy43-2.jpg
## [ 139 / 142 ] sy43-3.jpg
## [ 140 / 142 ] sy43-4.jpg
## [ 141 / 142 ] sy43-5.jpg
## [ 142 / 142 ] sy43-6.jpg
## Done in 14.8 secs
# add attributes
data.out <- Out(outlines,
fac = att.data)
# scale, align, rotate, and center specimens
norm.outlines <- data.out %>%
coo_scale() %>%
coo_align() %>%
coo_rotate() %>%
coo_center()
Calibrate harmonic + EFA
# calibrate how many harmonics needed
calibrate_harmonicpower_efourier(norm.outlines,
nb.h = 30)
## $gg
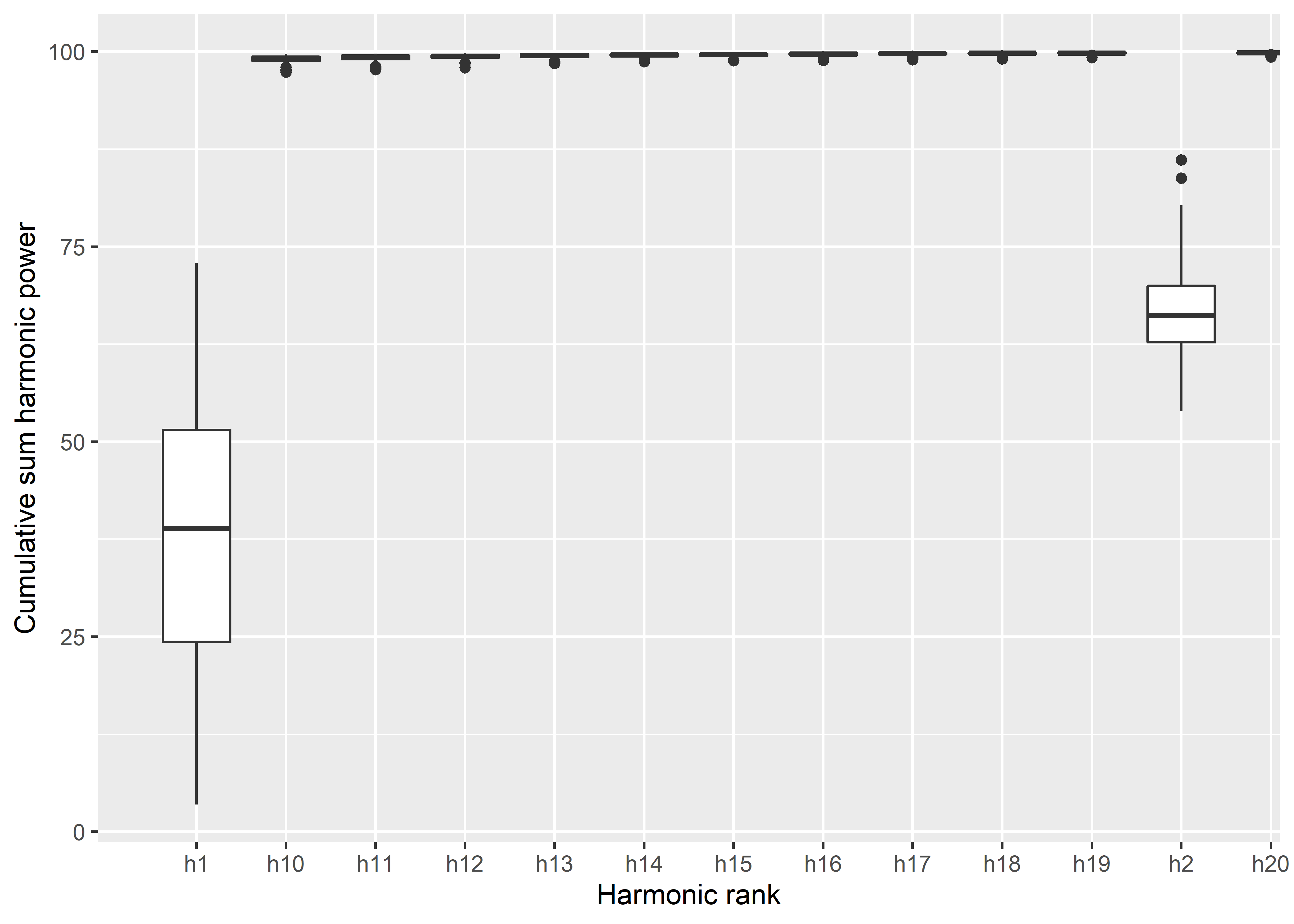
##
## $q
## h1 h2 h3 h4 h5 h6 h7 h8 h9 h10 h11 h12 h13 h14 h15 h16
## 489 72.808791 83.78198 95.17554 95.58620 96.94914 97.61501 97.95870 98.99222 99.27944 99.61408 99.66292 99.67257 99.74548 99.77200 99.80462 99.82192
## 490 64.114719 71.74229 80.72420 89.12673 91.89527 97.25527 97.89054 98.43317 98.90168 99.21067 99.26009 99.39885 99.47944 99.54422 99.59587 99.62522
## 553 60.227643 67.66112 78.47978 88.42469 91.97133 97.96056 98.60926 99.03073 99.36751 99.44516 99.53735 99.61913 99.67585 99.71820 99.75627 99.77140
## 554 40.784025 62.70509 71.02441 88.80778 92.02025 97.18926 98.19496 98.35599 98.99227 99.07903 99.18155 99.65220 99.70881 99.74345 99.82060 99.82265
## 555 71.883368 75.67063 83.98654 89.34967 91.27061 96.88514 98.02617 99.22945 99.34429 99.35722 99.65024 99.70336 99.74050 99.84641 99.86700 99.89300
## 556 40.131674 62.71068 66.15981 84.78732 88.45546 94.74772 96.20115 97.07108 98.32436 98.35603 98.48074 98.91994 99.09404 99.22256 99.33403 99.42302
## 558 63.012149 77.73567 90.06870 90.36598 91.90045 93.94937 94.75257 97.47642 98.23127 99.15827 99.24117 99.41253 99.50428 99.56908 99.72318 99.74806
## 559 37.440231 60.66242 71.29934 86.72881 90.17083 96.07668 97.22067 97.71586 98.44616 98.50390 98.65258 99.15941 99.41700 99.61239 99.65349 99.69833
## 562 60.694645 69.96634 77.12798 87.14123 90.12571 96.20471 97.29606 98.57226 99.03098 99.22437 99.49559 99.52488 99.55208 99.75261 99.77378 99.82801
## 565 64.493270 80.33025 89.87705 90.69617 92.26710 94.75796 95.81031 98.49869 99.02328 99.61277 99.62274 99.65681 99.75540 99.77200 99.81405 99.84130
## 591 32.410597 64.36665 71.82945 90.72323 94.12426 97.00883 98.55887 98.61906 98.76021 99.38794 99.56447 99.69590 99.74709 99.77566 99.78641 99.87133
## 598 54.095190 69.79342 80.21895 91.62848 93.17747 97.30424 98.48432 98.73772 99.23659 99.27576 99.30295 99.50219 99.52999 99.55235 99.69048 99.74154
## 645 37.430706 61.77266 70.12401 88.30539 92.41149 97.17813 98.23178 98.46989 98.73442 98.95378 99.08073 99.40631 99.44517 99.47290 99.55845 99.56258
## 646 48.472059 67.04623 73.39793 90.58139 94.34818 96.89540 98.59301 98.84265 99.02189 99.39947 99.48570 99.57729 99.68552 99.70816 99.72993 99.80558
## 647 63.962317 66.40189 73.20076 87.28925 92.34106 97.84810 98.43246 98.57160 99.16726 99.23451 99.33657 99.54623 99.61790 99.66645 99.73749 99.75055
## 648 51.661887 60.75373 67.73491 84.11689 90.80362 96.67577 97.48979 97.90301 98.89001 98.98484 99.05226 99.30660 99.42561 99.52725 99.64522 99.65408
## 649 13.198214 67.02359 73.20792 91.32686 96.27920 97.08839 97.94181 98.50792 98.74961 99.32895 99.45088 99.48496 99.54428 99.68207 99.72057 99.77413
## 650 62.500557 67.69024 73.36673 89.73518 94.63252 98.08290 98.54933 98.77696 99.31998 99.46525 99.56771 99.71114 99.72319 99.74218 99.76137 99.77677
## 651 25.861992 55.85938 68.03343 87.64255 92.73702 96.70377 98.18765 98.36471 98.70513 99.13669 99.30682 99.42507 99.45162 99.50142 99.52530 99.60766
## 652 22.576477 60.60679 68.19757 89.37573 93.98487 96.56320 97.92897 98.12207 98.20926 99.08563 99.26329 99.35190 99.43444 99.46619 99.51808 99.67351
## 653 53.506327 62.33004 70.77582 88.94387 93.68013 97.88528 98.55523 98.78018 99.26962 99.35380 99.44214 99.64394 99.65243 99.71399 99.78507 99.82541
## 654 44.031205 66.31590 73.29146 91.93527 95.20683 97.46861 98.89531 98.97063 99.04404 99.48813 99.58569 99.67358 99.74212 99.75227 99.76880 99.82519
## 655 53.169643 60.43443 64.83868 83.34328 89.55824 96.76372 97.87205 98.10188 99.14485 99.17562 99.18710 99.55622 99.62697 99.74582 99.74946 99.76780
## 656 57.110466 63.11221 68.16400 82.60450 87.07412 95.61119 97.38995 98.24966 99.07245 99.19652 99.44583 99.52592 99.55966 99.75749 99.77316 99.80910
## 657 44.153580 55.01196 61.02296 82.80466 87.94802 95.93126 97.01850 97.71437 98.65702 98.74675 98.81958 99.36470 99.57875 99.72769 99.75758 99.77069
## 658 61.749011 65.60642 71.58815 87.75926 93.23432 98.24621 98.52779 98.82481 99.43320 99.46738 99.50607 99.77579 99.82474 99.84460 99.85641 99.86427
## 659 50.938090 63.91895 68.76493 86.94809 89.69221 95.89946 97.42615 98.12618 99.17514 99.18318 99.26235 99.62159 99.66360 99.70855 99.81597 99.83027
## 660 44.673501 62.32531 67.80680 90.92520 94.83023 96.73639 98.51319 98.64637 98.72393 99.36060 99.56113 99.71252 99.74223 99.74241 99.75423 99.80213
## 661 48.318800 59.00113 64.26505 85.67911 90.52577 96.55592 97.60929 98.05560 98.94426 98.98235 99.00026 99.45111 99.52906 99.58658 99.67788 99.69162
## 665 72.904144 75.33543 80.78979 88.20015 91.08371 97.41274 98.34543 99.00547 99.29183 99.36726 99.57786 99.63159 99.67359 99.78074 99.78648 99.80747
## 677 43.622937 58.91874 66.48334 89.42983 93.54165 96.83488 98.47343 98.69266 98.80843 99.14402 99.27266 99.54711 99.57613 99.60539 99.62761 99.71459
## 678 70.247711 71.42578 81.10140 86.84716 90.52952 96.31749 98.02421 99.25218 99.33627 99.38623 99.56052 99.60291 99.61013 99.70996 99.78256 99.78790
## an115-fig7 52.227029 66.03736 74.39393 88.54440 91.97779 97.28538 98.37656 98.66908 99.30542 99.38414 99.42461 99.61270 99.62449 99.62990 99.65750 99.66926
## an51-fig26a 20.037123 58.27095 69.00891 87.33896 90.87947 95.25013 97.25337 97.51169 97.69137 98.00853 98.43021 98.56876 98.89093 99.10015 99.37975 99.45431
## h17 h18 h19 h20 h21 h22 h23 h24 h25 h26 h27 h28 h29
## 489 99.82341 99.85272 99.87865 99.91085 99.92286 99.94669 99.96596 99.98339 99.98504 99.99251 99.99371 99.99574 100
## 490 99.63711 99.71079 99.75015 99.75947 99.78940 99.82367 99.86219 99.92748 99.93455 99.96848 99.98226 99.99078 100
## 553 99.78933 99.81395 99.83675 99.88522 99.89000 99.92227 99.92644 99.93262 99.94819 99.97288 99.98151 99.98828 100
## 554 99.84003 99.88827 99.89508 99.90968 99.92937 99.94159 99.94846 99.96047 99.97359 99.97812 99.98289 99.98863 100
## 555 99.92314 99.94175 99.96739 99.96955 99.97635 99.97732 99.98256 99.98329 99.99026 99.99125 99.99440 99.99454 100
## 556 99.55630 99.59933 99.63249 99.66365 99.69817 99.72227 99.73924 99.75857 99.78090 99.83743 99.87875 99.97544 100
## 558 99.78242 99.84868 99.86327 99.88367 99.90459 99.90700 99.92415 99.93280 99.97915 99.98029 99.98517 99.99161 100
## 559 99.74681 99.79044 99.80719 99.82695 99.87185 99.89070 99.93852 99.94821 99.96116 99.97516 99.98627 99.99001 100
## 562 99.85958 99.86190 99.88385 99.89866 99.90624 99.93707 99.94290 99.95298 99.95893 99.97706 99.97944 99.99213 100
## 565 99.86763 99.88482 99.92366 99.94140 99.95881 99.96587 99.98508 99.98571 99.98634 99.99102 99.99496 99.99815 100
## 591 99.87713 99.88817 99.92076 99.92919 99.94188 99.95569 99.96000 99.96944 99.97262 99.98283 99.98986 99.99933 100
## 598 99.75481 99.81876 99.87467 99.87899 99.89069 99.90750 99.93148 99.94348 99.97319 99.97965 99.99165 99.99538 100
## 645 99.59820 99.71182 99.76571 99.83101 99.88606 99.91024 99.91251 99.92711 99.93754 99.94735 99.96603 99.96636 100
## 646 99.82420 99.83787 99.86296 99.89529 99.89981 99.94561 99.94999 99.95108 99.96046 99.96673 99.97721 99.98563 100
## 647 99.76713 99.77742 99.84435 99.86703 99.88193 99.92977 99.95002 99.95551 99.97231 99.97771 99.97981 99.99703 100
## 648 99.70820 99.73725 99.76721 99.84772 99.86568 99.89290 99.92611 99.92919 99.94981 99.96239 99.98568 99.99734 100
## 649 99.79398 99.81656 99.84928 99.87351 99.88844 99.90363 99.90763 99.93084 99.94448 99.96397 99.97705 99.98854 100
## 650 99.79153 99.81017 99.88066 99.88864 99.92889 99.95128 99.95697 99.95804 99.97550 99.97808 99.98663 99.99276 100
## 651 99.64903 99.71442 99.72953 99.80386 99.82414 99.83815 99.86617 99.91585 99.92272 99.96878 99.97907 99.98814 100
## 652 99.77700 99.78891 99.84286 99.85576 99.90064 99.93449 99.93964 99.94659 99.96045 99.96570 99.97796 99.97914 100
## 653 99.84104 99.87795 99.89456 99.89757 99.90810 99.92429 99.94213 99.94952 99.96145 99.96616 99.97349 99.98101 100
## 654 99.84526 99.85335 99.87885 99.89331 99.91234 99.93124 99.94158 99.94476 99.95093 99.97372 99.98650 99.99498 100
## 655 99.77633 99.81093 99.85482 99.87491 99.91767 99.92153 99.93546 99.95328 99.96402 99.97827 99.98215 99.98870 100
## 656 99.81796 99.84004 99.84539 99.89515 99.90107 99.90748 99.93264 99.93569 99.95801 99.96491 99.98486 99.99717 100
## 657 99.78894 99.81597 99.84526 99.85987 99.87213 99.90453 99.93306 99.95702 99.97221 99.97408 99.99000 99.99282 100
## 658 99.86832 99.91702 99.93080 99.94344 99.95814 99.95937 99.96680 99.97460 99.98321 99.98500 99.99520 99.99921 100
## 659 99.84733 99.86700 99.87883 99.88528 99.90467 99.91397 99.94898 99.95854 99.96858 99.97314 99.98438 99.99169 100
## 660 99.82431 99.83041 99.85408 99.87850 99.89197 99.91011 99.92247 99.94037 99.95445 99.97124 99.97581 99.98600 100
## 661 99.70964 99.76618 99.81364 99.85320 99.88166 99.88563 99.89367 99.91834 99.93786 99.95715 99.98864 99.99733 100
## 665 99.84066 99.85990 99.86897 99.90740 99.90987 99.92833 99.94610 99.95185 99.96528 99.97796 99.98729 99.99499 100
## 677 99.77934 99.78599 99.82397 99.84851 99.87206 99.93771 99.93980 99.94562 99.95115 99.96424 99.97163 99.99565 100
## 678 99.85325 99.87332 99.89596 99.90323 99.92267 99.93005 99.94635 99.95250 99.96118 99.96790 99.97532 99.98628 100
## an115-fig7 99.67207 99.72294 99.75347 99.78824 99.82672 99.85442 99.89998 99.95409 99.96209 99.96910 99.97535 99.99002 100
## an51-fig26a 99.66639 99.75295 99.78979 99.81799 99.83093 99.84700 99.86316 99.89490 99.93231 99.96307 99.96865 99.99647 100
## [ reached getOption("max.print") -- omitted 108 rows ]
##
## $minh
## 90% 95% 99% 99.9%
## 6 7 11 23
# 11 harmonics needed to capture 99 percent of variation
calibrate_reconstructions_efourier(norm.outlines,
range = 1:11)
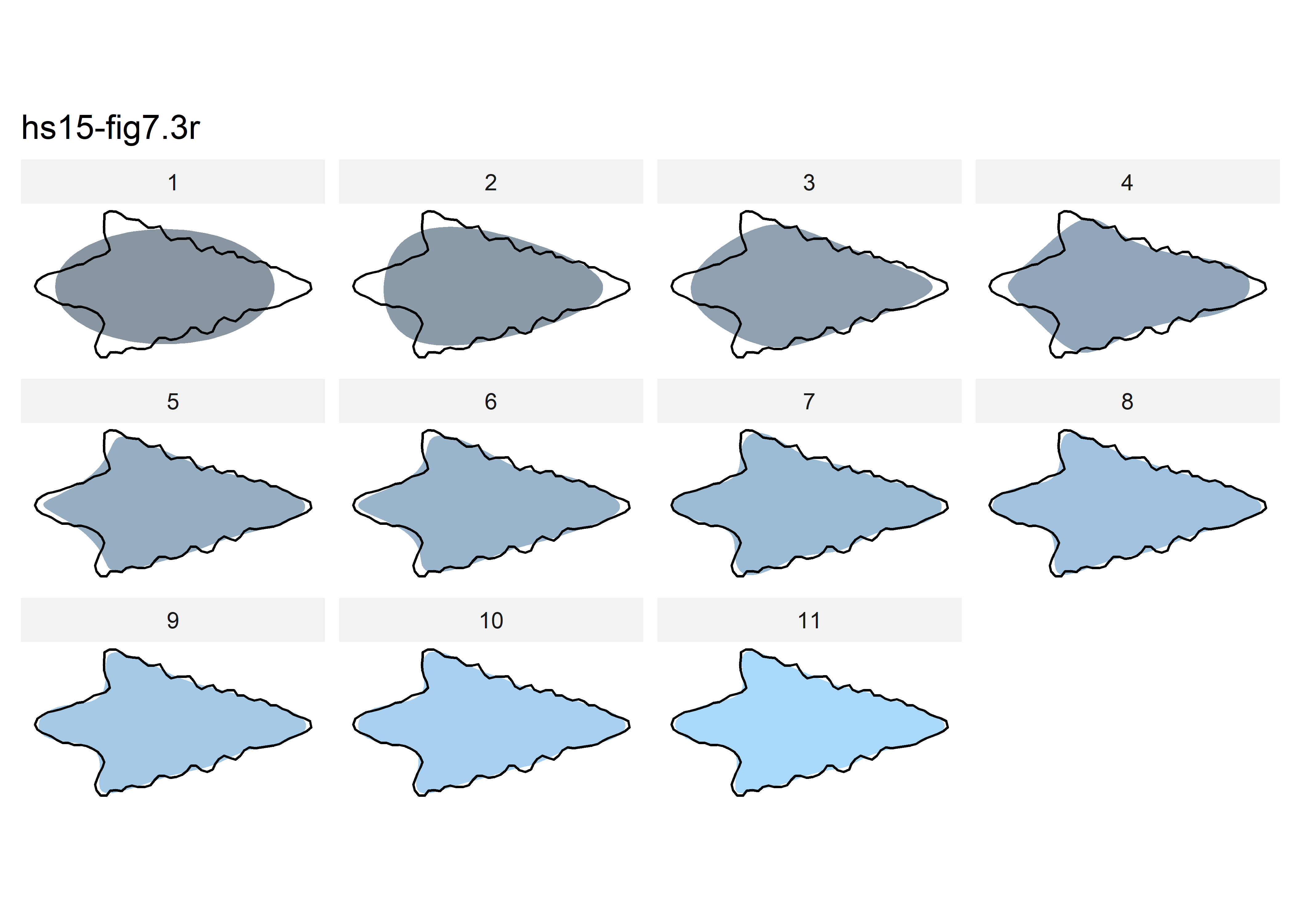
# generate efa outlines with 11 harmonics
efa.outlines <- efourier(norm.outlines,
nb.h = 11,
norm = TRUE)
# use efa.outlines for pca
pca.outlines <- PCA(efa.outlines)
PCA
# pca
scree_plot(pca.outlines)
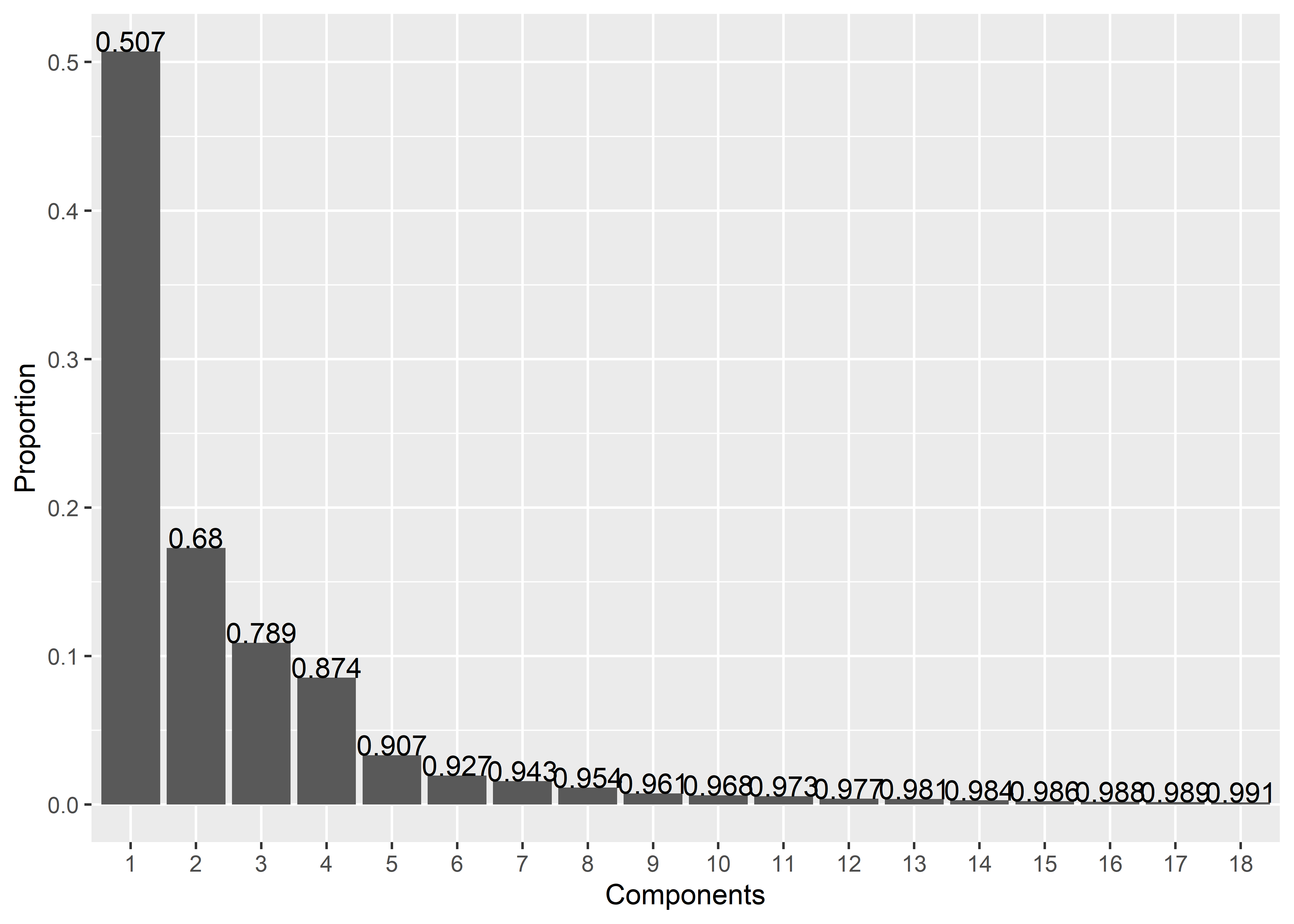
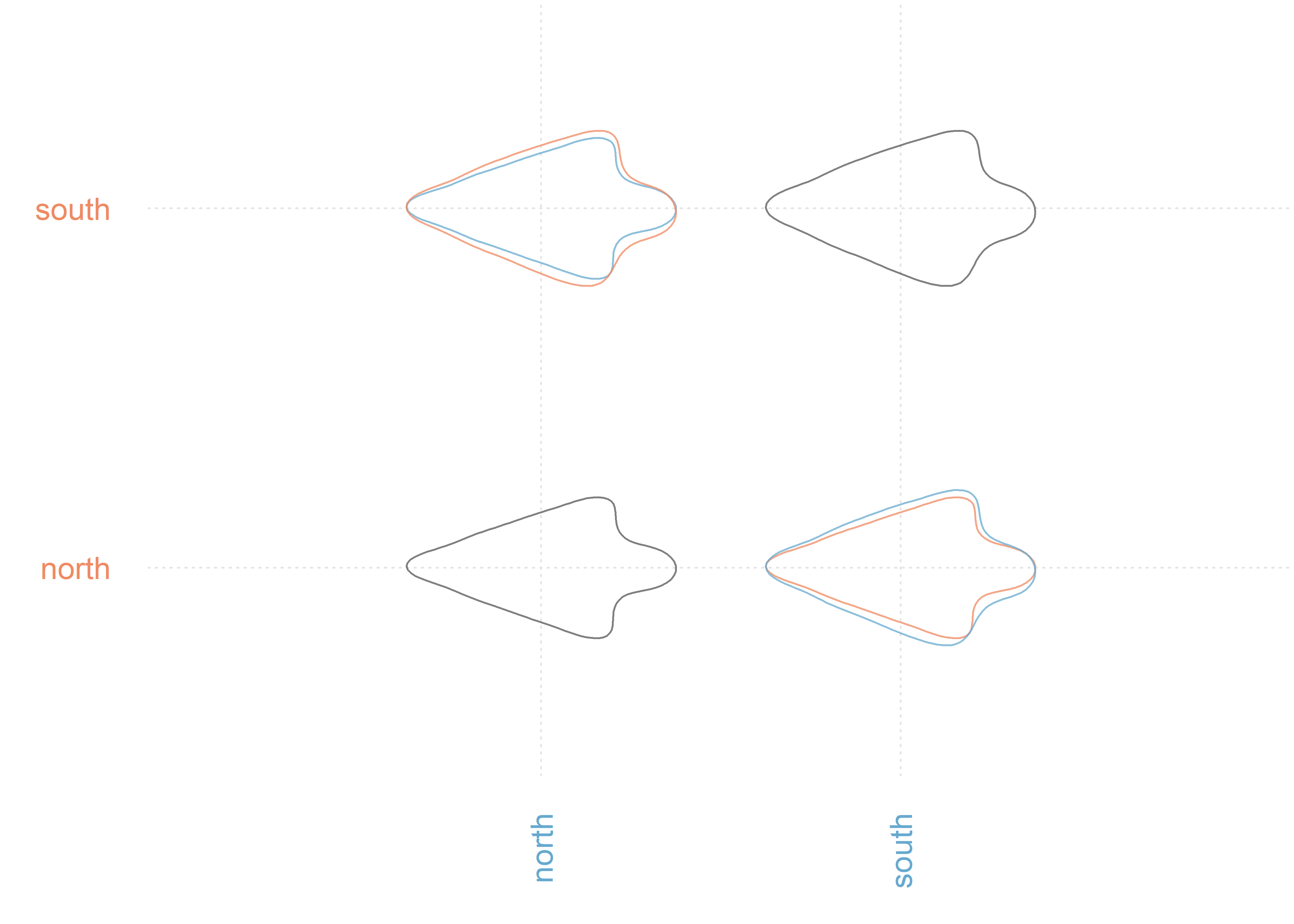
# plot pca by region
plot_PCA(pca.outlines,
morphospace_position = "range",
palette = pal_qual_solarized,
chullfilled = TRUE,
~region,
axesnames = TRUE,
morphospace = TRUE,
eigen = TRUE,
center_origin = TRUE,
zoom = 1.4)
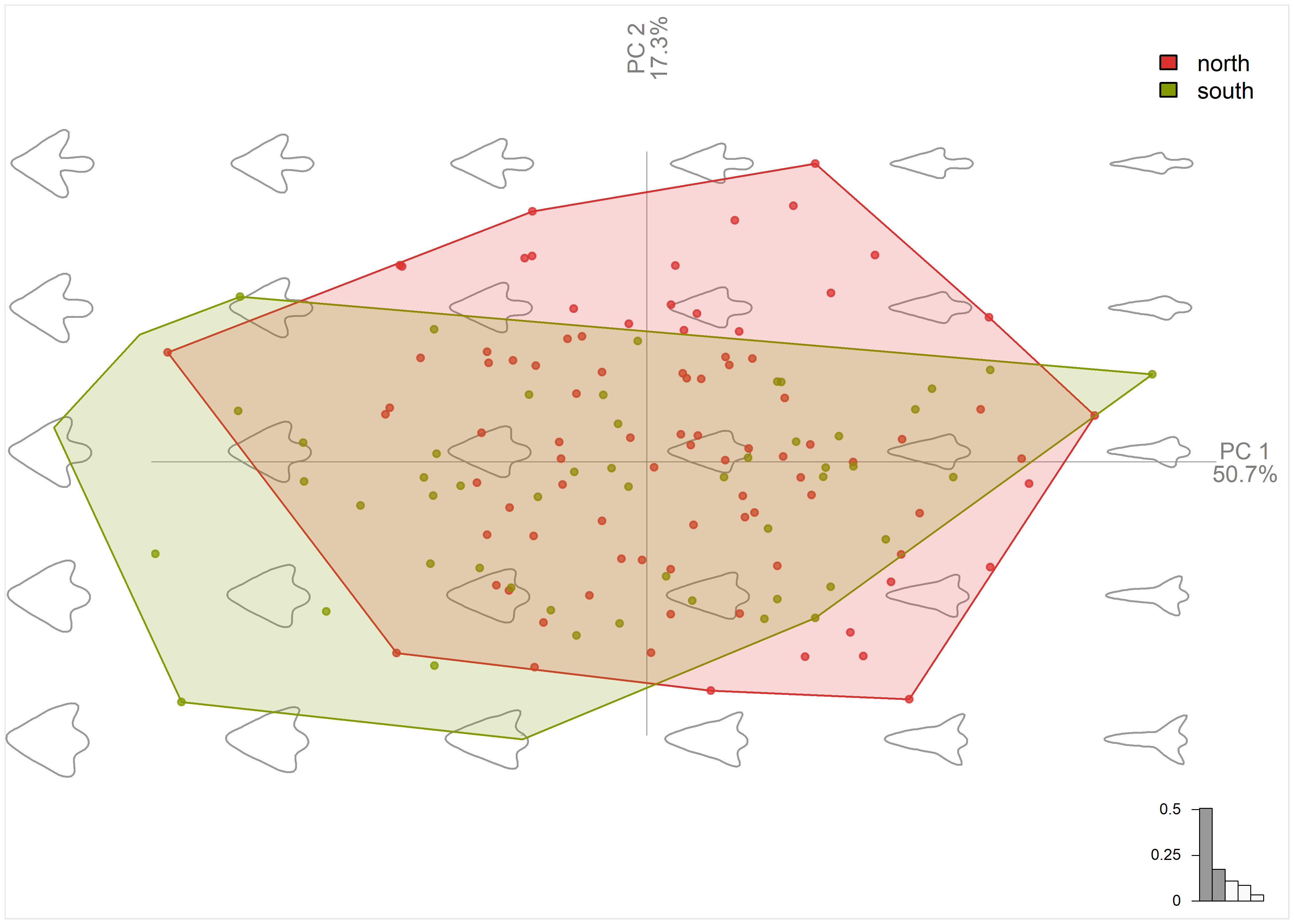
# plot pca by temporal + region
plot_PCA(pca.outlines,
morphospace_position = "range",
palette = pal_qual_solarized,
chullfilled = TRUE,
~temp.reg,
axesnames = TRUE,
morphospace = TRUE,
eigen = TRUE,
center_origin = TRUE,
zoom = 1.4)
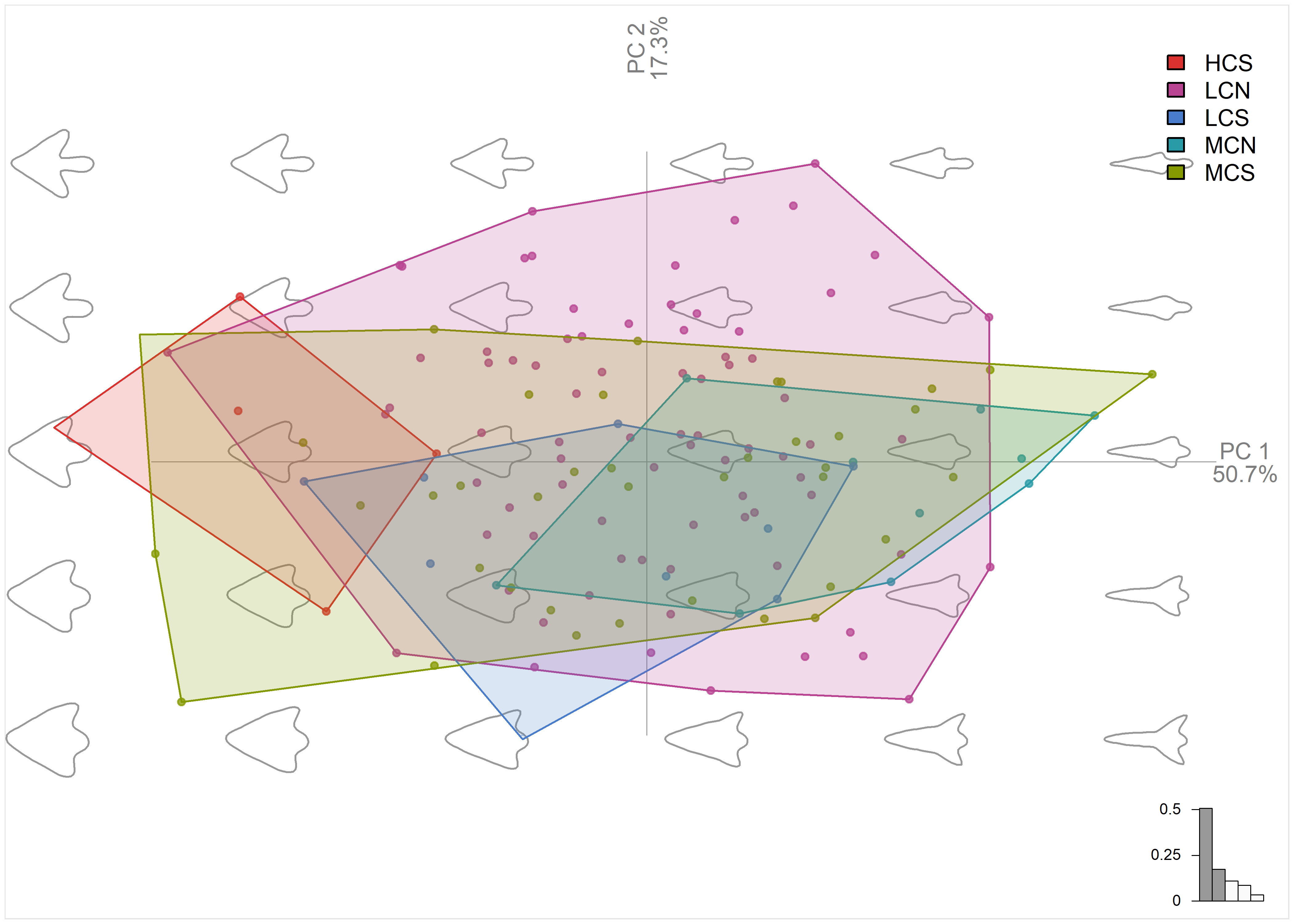
# mean shape + 2sd for the first 5 pcs
PCcontrib(pca.outlines, nax = 1:5)
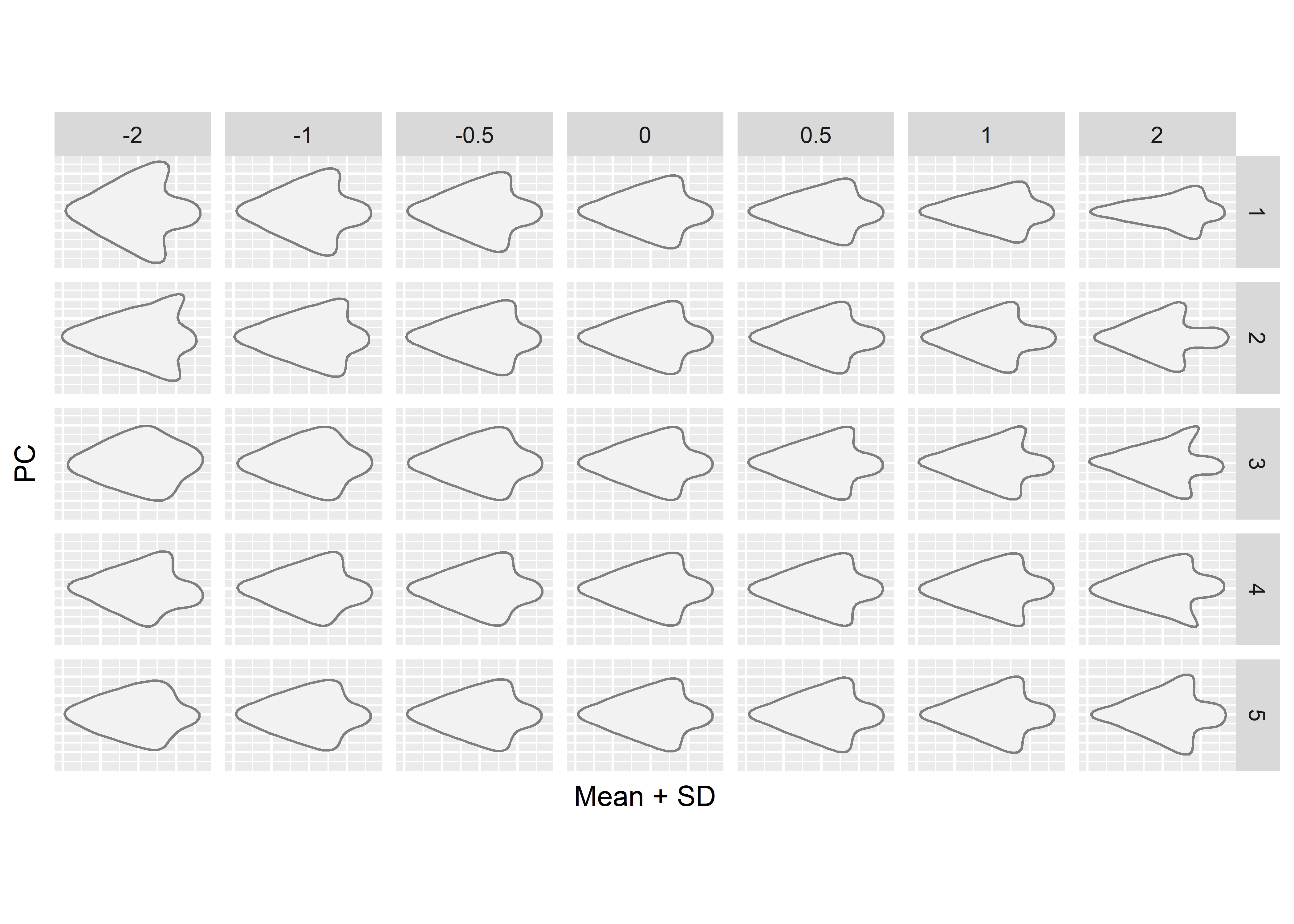
MANOVA + MANOVA_PW
# manova
# shape difference between temporal periods?
MANOVA(pca.outlines, 'region')
## PC axes 1 to 18 were retained
## Df Hotelling-Lawley approx F num Df den Df Pr(>F)
## fac 1 0.91 6.2183 18 123 1.424e-10 ***
## Residuals 140
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# shape difference between temp.reg?
MANOVA(pca.outlines, 'temp.reg')
## PC axes 1 to 18 were retained
## Df Hotelling-Lawley approx F num Df den Df Pr(>F)
## fac 4 2.5095 4.1302 72 474 < 2.2e-16 ***
## Residuals 137
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# which differ?
MANOVA_PW(pca.outlines, 'temp.reg')
## 'HCS' has 5 rows, and 'retain' is set accordingly
## PC axes 1 to 5 were retained
## HCSLCN
## HCSLCS
## HCSMCN
## HCSMCS
## LCNLCS
## LCNMCN
## LCNMCS
## LCSMCN
## LCSMCS
## MCNMCS
## $stars.tab
## HCS LCN LCS MCN MCS
## HCS *** - *** ***
## LCN ** *** ***
## LCS - -
## MCN *
##
## $summary (see also $manovas)
## Df Pillai approx F num Df den Df Pr(>F)
## HCS - LCN 1 0.4090 10.796 5 78 6.552e-08
## HCS - LCS 1 0.6060 2.461 5 8 1.236e-01
## HCS - MCN 1 0.9190 20.427 5 9 1.143e-04
## HCS - MCS 1 0.7445 22.146 5 38 2.484e-10
## LCN - LCS 1 0.2023 4.159 5 82 2.039e-03
## LCN - MCN 1 0.2322 5.019 5 83 4.566e-04
## LCN - MCS 1 0.3884 14.225 5 112 9.059e-11
## LCS - MCN 1 0.4733 2.336 5 13 1.011e-01
## LCS - MCS 1 0.1901 1.971 5 42 1.029e-01
## MCN - MCS 1 0.2462 2.809 5 43 2.786e-02